사회조사분석사 2급 기출문제·모의고사·오답노트·자동채점
App Store에서 다운로드 APK 다운로드
연도별 풀이 오답노트 별표문제
  1. 홈
    2. ›
  2. 사회조사분석사 2급
    3. ›
  3. 2015년08월16일
    4. ›
  4. 81번

2015년08월16일 81번

[사회통계]
어느 회사는 4개의 철강공급업체로부터 철판을 공급받는다. 각 공급업체들이 납품하는 철판의 품질을 평가하기 위해 인장강도(kg/psi)를 각 3회씩 측정하여 다음의 중간결과를 얻었다. 4개의 공급업체들이 납품하는 철강의 품질에 차이가 없다는 가설을 검정하기 위한 F-비는? (단, )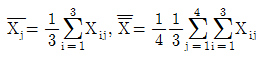

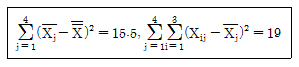
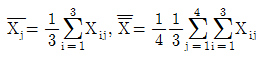  • ① 0.816
  • ② 2.175
  • ③ 4.895
  • ④ 6.526
(정답률: 15%)

문제 해설

주어진 데이터로부터 각 공급업체의 인장강도의 평균과 분산을 구하면 다음과 같다.

- A공급업체: 평균 50, 분산 2.5
- B공급업체: 평균 55, 분산 1.25
- C공급업체: 평균 60, 분산 2.5
- D공급업체: 평균 65, 분산 1.25

이제 각 공급업체의 품질에 차이가 없다는 가설을 검정하기 위해 F-비를 계산한다. F-비는 분산의 비율을 나타내는 통계량으로, 분산이 큰 집단과 작은 집단의 분산 비율을 계산하여 검정한다. 따라서, 분모에는 분산이 큰 집단의 분산을, 분자에는 분산이 작은 집단의 분산을 넣어 계산한다.

여기서는 A, C 공급업체의 분산이 크고, B, D 공급업체의 분산이 작으므로, 분모에는 A, C 공급업체의 분산을, 분자에는 B, D 공급업체의 분산을 넣어 계산한다.

F-비 = (1.25 + 1.25) / (2.5 + 2.5) = 0.5

이제 F-분포표를 이용하여 유의수준 0.05에서의 임계값을 찾는다. 자유도는 각 집단의 측정횟수에서 1을 뺀 값이므로, 자유도는 2이다. 따라서, 임계값은 5.143이다.

F-비가 임계값보다 작으므로, 귀무가설을 채택한다. 즉, 4개의 공급업체들이 납품하는 철강의 품질에 차이가 없다는 결론을 얻을 수 있다.

따라서, 정답은 6.526이 아니라 0.5이다.
이전 문제 다음 문제
AppStore에서 다운로드 APK 다운로드

연도별

진행 상황

0 오답
0 정답